14. březen - Den π - mezinárodní den matematiky
Tento mezinárodní den se slaví 14. března. V anglicky mluvících zemích toto datum zapisují 3.14 (3. měsíc, 14. den). A to je vyjádření hodnoty tzv. Ludolfova čísla π, které udává poměr obvodu kruhu k jeho průměru [π=3,14159265358979323846…] Vzorce k vypočítání π mají požadované matematické vlastnosti, ale jsou těžko pochopitelné bez znalosti trigonometrie. Při studiu na střední škole jsme občas (pro větší přesnost) používali zlomek dvacet dva sedmin.
Kdo byl vlastně zakladatelem matematiky? Muž, žijící pravděpodobně v letech 624 až 548 př. n. l. Jmenoval se Thales a pocházel z Milétu v Iónii v Malé Asii v jihozápadním cípu tehdy řeckého, dnes tureckého města ležícího poblíž Středozemního moře nedaleko Izmiru. Tam tehdy žil tento intelektuál a bádal, až objevil zajímavou věc (zde se mnou asi ne všichni žáci osmých tříd ZŠ budou souhlasit) – zajímal se o trojúhelník a kružnici a sdělil lidstvu větu, které se dala tesat do kamene. Thaletova věta je matematická věta o velikosti úhlů trojúhelníků vytvořených nad průměrem kružnice. Kružnice, která je součástí konstrukce Thaletovy věty, bývá označována jako Thaletova kružnice.
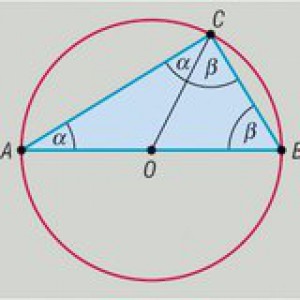
Všechny obvodové úhly sestrojené nad průměrem kružnice jsou pravé. Jiné znění: Všechny trojúhelníky, jejichž nejdelší stranu půlí střed kružnice opsané, jsou pravoúhlé. Nebo jinak: Sestrojme libovolnou kružnici k s průměrem d. Koncové body jejího průměru označme A a B a zvolme libovolný bod C na kružnici k. Pak platí, že trojúhelník ABC je pravoúhlý a má pravý úhel u vrcholu C.
Původní znění zřejmě bylo: Velikost středového úhlu je rovna dvojnásobku velikosti obvodového úhlu příslušného témuž oblouku (při středovém úhlu 180° – přímka, je obvodový úhel pravý – 90°). Nebo ještě jinak: Máme-li tři body A, B a C na kružnici k se středem O, potom úhel ∠AOC je dvakrát větší než úhel ∠ABC.
Thales z Milétu ale zřejmě nebyl první, kdo tuto větu vyslovil. Byla známá již Egypťanům a Babyloňanům, ačkoliv ti ji znali jen ze zkušenosti, nedokázali ji. To udělal právě až Thales, který využil znalostí toho, že úhly při základně rovnoramenného trojúhelníku mají stejnou velikost a součet úhlů v trojúhelníku je roven dvěma pravým úhlům /180°/.
Thaletovi je připisována řada mravních naučení, životních rad a mou-drých výroků jako například: Poznej sebe sama. Záruka, to je zkáza. Jsou-li u tebe přátelé, pamatuj i na ty, kteří u tebe nejsou. Nepřikrášluj svůj vzhled, nýbrž buď krásný způsobem života. Neobohacuj se špatným způsobem. Nerozpakuj se lichotit rodičům. Nepřebírej od otce jeho špatnosti. Trapná je nečinnost, škodlivá nemírnost, obtížná nevzdělanost. Nebuď líný, ani když jsi bohatý. Uč se a vyučuj to lepší. Vzbuzuj spíše závist než soucit. Nevěř všemu a všem. Vládneš-li, udržuj se v řádu. Na otázku, co je nesnadné, odpověděl: „Poznat sebe sama“. Kdo je blažený? Ten, kdo je tělesně zdráv, duševně bystrý a má dobrou povahu. Jaké služby prokážeš svým rodičům, takové očekávej i od svých dětí. Jak žít nejlépe a nejspravedlivěji? Kdybychom sami nedělali to, co vytýkáme ostatním…
Archimedes byl prvním člověkem, který za pomoci vepsaných a opsaných mnohoúhelníků a výpočtem jejich obvodů řešil číslo π. Při použití 96úhelníka dokázal, že hodnota 223/71 je menší než π a to je menší než 220/70. Získaný výpočet se přibližně rovnal 3,1415...
Přestože je hodnota čísla π pevně stanovena, jedná se o takzvané iracionální číslo. To znamená, že jej nelze přesně vyjádřit jako zlomkem stanovený podíl dvou celých čísel. Zároveň jej nelze konečným způsobem vyjádřit v desítkové soustavě, a to ani za pomoci periody. V uplynulých dekádách vědci, matematici a počítačoví odborníci postupně dopočítávali hodnotu π na tisíce, miliony a pak i biliony desetinných míst. Dosud poslední doložený rekord stanovil Jordan Raonus ze Cincinnati na konci června 2024. V Storage Review Lab publikoval dosud nejpřesnější odhad hodnoty tohoto čísla v desítkové soustavě, a to přesně na 202 112 290 000 000 desetinných míst. Výpočet mu zabral celých 104 dní.
Řecké písmeno π pro označení tohoto čísla použil poprvé velšský matematik William Jones v roce 1706, o jeho další popularizaci se pak postaral neméně známý švýcarský matematik Leonhard Euler v roce 1737. Nicméně dnes se mu většinou říká Ludolfovo číslo podle Ludolpha van Ceulena (1540-1610), který výpočtu této konstanty věnoval značnou část svého života a číslo 3,14159265358979323846264338327950288… si v této podobě nechal vytesat i na svůj náhrobek.
V anglosaském světě a v ranější historii se pro číslo π používalo i označení Archimédova konstanta. Právě řecký matematik Archimédés ze Syrakus byl první, kdo odhadl π "skoro přesně". Nicméně o možné znalosti π se spekuluje již u starověkých Egypťanů v období Staré říše (přibližně 2700-2181 před Kristem - viz výše), a to na základě rozměrů pyramid, ve kterých už bylo "zakódováno" - například Velká pyramida v Gíze byla postavena s obvodem 1760 loktů a s výškou 280 loktů. Navržený poměr 1760/280, tedy 44/7, je roven přibližně hodnotě 2π.
Zkoumání a výpočtům π se věnovalo několik významných matematiků starověku či raného středověku jako Ptolemaios, Apollónios z Pergy, Liou Chuej, Cu Čchung-č’ či Moše ben Mamon, později Isaac Newton, Johann Heinrich Lambert a další.

